It has been generally recognized that accurate horizontal gradients of Integrated Water Vapor (IWV) content of the atmosphere are obtained from measurements made by the GPS receivers of a geodetic network. However, no derivative of any observed atmospheric parameter can be made of use as such in the operational data-assimilation of Numerical Weather Prediction (NWP). Thus, an overall absolute level of the IWV contents has to be estimated accurately in one way or another. This, in turn, means that both the geodetic and all meteorological measurements involved must be properly adjusted i.e. statistically calibrated according to best possible standards in real- or near-real-time.

Near-optimal Kalman Filters (KF) are generally used for "built-in calibration" of GPS and other general-purpose navigation receivers. However, the computing load of the inversion problem of optimal Kalman filtering is proportional to the cubic of the data volumes that need simultaneous processing. This computing requirement has so far gone beyond all manageable limits for many sophisticated observing systems like those of NWP (Gal-Chen, 1988). A relatively general and Fast way of computing Kalman Filters (FKF) for real- time Optimum Calibration (O/C) of meteorological observations has been developed (Lange, 1999). FKF should also apply to an operational "built-in calibration" of the IWV measurements and possibly to the geodetic GPS networks themselves.

The joint regression equation system for all different observations can be written in the Canonical Block-Angular (CBA) form as follows:

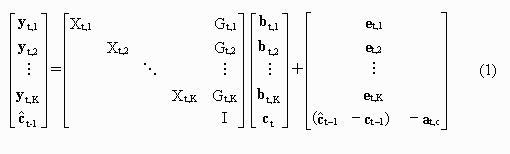
where vectors y_t,1, y_t,2,…, y_t,K and e_t,1, e_t,2,…, e_t,K represent measurements and residuals, respectively, from K more or less dependent observation series during an observing period t (t = 1, 2,…). Vectors b_t,1, b_t,2,…, b_t,K represent all those parameters that are normally "pre- eliminated" by the Bernese GPS Software (Brockmann, 1996). The unknown parameters are represented here by a common vector c_t. Matrices X_t,1, X_t,2,…, X_t,K and G_t,1, G_t,2,…, G_t,K are the Jacobians that are related to the "pre-eliminated" parameters and the common unknown parameters, respectively. Vector a_t,c represents all those noise terms that stem from calibration drifts.

After an orthonormalization of measurement errors e_t,1, e_t,2,…, e_t,K is made separately within each observation series k (k = 1, 2,…, K) the optimal Least Squares Estimates (LSE) can be computed as follows:

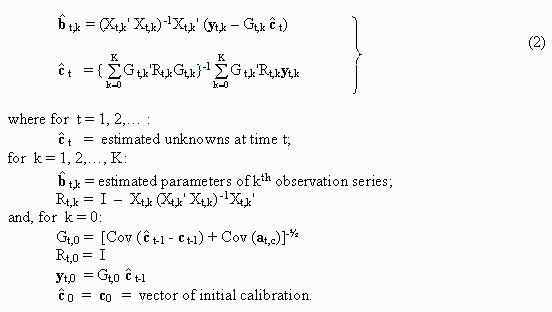
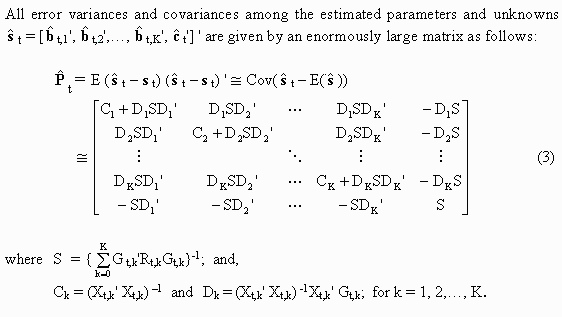
The main advantage of these FKF formulas (2) is that the enormous joint Normal Equation (NEQ) system was solved semi-analytically. Extremely large windows of data can now be analyzed in real- time for improved estimation of unknown parameters that may otherwise not be observable.

The Statistical Calibration software applies also to post-processing of comprehensive innovation sequences i.e. the difference data from GPS networks, the meteorological data from upper-air sounding stations and the departure data from HIRLAM runs, etc.. The sophisticated statistical method of Minimum Norm Quadratic Unbiased Estimation (MINQUE) can be used for computing error variances and covariances (Rao, 1972). A suitable set of the various parameters needs first to be identified before operational implementation. Optimum Interpolation (O/I) and 3- or 4-DVAR data-assimilation require these estimates for optimal exploitation of the GPS measurements.

Helmert, F. R., Die mathematischen und physikalischen Theorien der höheren 
Geodäsie, 1. Teil,  Leipzig, 1880.

Kalman, R. E., A New Approach to Linear Filtering and Prediction Problems. 
Trans. ASME J. of Basic Eng., 82-D, pp. 35-45, 1960. 

Kalman, .R. E. and Bucy, R. S., New Results in Linear Filtering and Prediction Theory. 
Trans. ASME J. of Basic Eng., 83-D, pp. 95-108, 1961. 

Lange, A. A., Kanonisen analyysin laskennoista, Laskentakeskuksen  
Tiedonantoja, No. 1, Jyväskylän Yliopisto, 1969.

Rao, C. R., Estimation of variance and covariance components in linear models, 
J. Am. Stat. Assoc., Vol. 67, No. 337, pp. 112-115, 1972. 

Wolf, H., The Helmert block method, its origin and development, 
Proceedings of the Second International Symposium on Problems 
Related to the Redifinition of North American Geodetic Networks, 
Arlington, Va. April 24-28, pp. 319-326, 1978.

Lange, A. A., Multipath propagation of VLF Omega signals, 
IEEE PLANS '82 - Position Location and Navigation Symposium Record, 
December 1982, pp. 302-309, 1982. 

Lange, A. A., A high-pass filter for optimum calibration of observing systems 
with applications, In: Simulation and optimization of large systems, 
edited by Andrzej. J. Osiadacz, Clarendon Press, Oxford, pp. 311-327, 1988.

Gal-Chen, T., et al., Report of the Critical Review Panel - Lower Tropospheric 
Profiling Symposium: Needs and Technologies,  
Bull. Am. Met. Soc., Vol. 71, No. 5, pp. 680-687, 1990. 

Brockmann, E., Combination of solutions for geodetic and geodynamic 
applications of the Global Positioning System (GPS), 
Geodätisch - geophysikalische Arbeiten in der Schweiz, Volume 55, 
Schweitzerische Geodätische Kommission, 1997.

Strang, G. and Borre, K., Linear Algebra, Geodesy, and GPS, 
Wellesley-Cambridge Press, 1997.

Lange, A. A., Statistical calibration of observing systems, 
Contributions, No. 22, Finnish Meteorological Institute, 
Helsinki, Finland, 1999.

Lange, A. A., Simultaneous Statistical Calibration of the GPS signal delay measurements with related meteorological 
data, Phys. Chem. Earth (A), Vol. 26, No. 6-8, pp. 471-473, 2001.