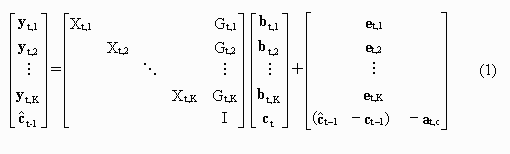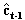 .
Matrices Xt,1, Xt,2,…, Xt,K and Gt,1, Gt,2,…, Gt,K
are the Jacobians that are related to the unknown parameters and to the common parameters,
respectively.
Vector at,c represents random errors of the common parameters
that typically stem from various calibration drifts and/or modeling errors.
.
Matrices Xt,1, Xt,2,…, Xt,K and Gt,1, Gt,2,…, Gt,K
are the Jacobians that are related to the unknown parameters and to the common parameters,
respectively.
Vector at,c represents random errors of the common parameters
that typically stem from various calibration drifts and/or modeling errors. Moreover, it is possible to determine an additional set of common parameters for transforming the joint covariance matrix of the residuals et,1, et,2,…, et,K into a strictly block-diagonal form. This can be done by making use of those CANONICAL COMMON FACTORS (e.g. Empirical Orthogonal Functions Gt,1, Gt,2,…, Gt,K) that are found by performing a Principal Component Analysis on all the residuals after they have first been orthonormalized separately within every block k (k = 1, 2,..., K). This computational procedure for finding the conventional Canonical Correlations between only two blocks (K = 2) of data was described by Lange already in 1969. These tedious preparatory measures are required for speeding up the optimal FKF computations in realtime. Reference is also made to the discussion on Multivariate Statistical Methods in Statistical Calibration of Observing Systems (Lange, 1999), see page 16, and PCT/FI96/00621 (Lange, 1997), see pages 11-12.